Recentrer les idées en matière d'audio numérique

[gammaburst]

Je continue a voir de ci de là des erreurs de base sur le principe de l'audio numérique. Histoire de me défouler, et aussi de sonder un forum audiophile pour évaluer si la majorité à fait "le bon choix" dans le tri de ces idées, je vais me lancer dans un récapitulatif des principes. Pardon à ceux pour qui j'enfonce des portes ouvertes.

La majorité des discussions tournent autour de l'échantillonnage qui, à proprement parler, est une pratique purement analogique. On ne passe en numérique que si l'on décide de représenter les échantillons analogiques par des valeurs numériques, ce qui n'est pas une obligation. Un contre-exemple est fourni par le cinéma argentique, chaque image analogique sur la pellicule représentant un échantillon pris sur le mouvement continu. La théorie s'applique à ce cas avec les mêmes conclusions.

1) L'échantillonnage:

1.1) La capture
==========
On posera en préliminaire la chose fâcheuse suivante: il faut admettre qu'il y a des situations, en science et en technique, où l'intuition s'effondre complètement. Elle ne voit pas, ne comprend pas ce qui se passe. Pire encore, elle affirme avec aplomb et certitude des choses qui sont totalement fausses. Si j'en parle, c'est bien entendu que la théorie de l'échantillonnage en est un exemple typique.

En l'absence de l'intuition pour guide, que reste-t-il ? Les maths ! (Aaarghhh!) Mais rassurez-vous, pas de formules dans cette explication, je me contenterai de donner les conclusions.

Donc, pour paraphraser Dante: "Vous qui entrez ici, laissez toute intuition".

Procédons donc: on part d'une modélisation du son comme une fonction continue, représentant typiquement l'évolution dans le temps du signal électrique qui sort du micro. L'analogique (magnétique ou vinyle), stocke la continuité de cette courbe.
En numérique, on se contente de faire une mesure à intervalles régulier de l'amplitude du signal, que l'on convertit en un nombre qui sera stocké sur le support choisi, ou transmis. Chaque mesure constitue ainsi un échantillon de l'état du signal à l'instant t.

Une courbe continue comporte une infinité de points, mais les capturer tous demanderait une infinité de mesures realisées chacune en un temps infiniment court, produisant un débit numérique infini , et demandant un volume de stockage à l'avenant. On est donc obligé de se contenter d'une mesure à intervalles raisonables. Mais en est-on pénalisé pour autant ?

Ce qu'en dit l'intuition:
-------------------------
Il y a plein de trous entre les échantillons où l'information originelle a été perdue. Je devrai donc à la reproduction les boucher par interpolation en "reliant les pointillés" (les échantillons). J'obtiendrai une approximation d'autant plus proche de la réalité que la fréquence d'échantillonnage (le nombre d'échantillons par seconde) tend vers l'infini. Et bien avant cela, il viendra un moment où l'oreille humaine ne sera plus capable de déceler la différence. Mais dans ma tête d'audiopĥile, je sais que ce n'est qu'une approximation et ça me gêne. De plus, peut-être que le niveau d'approximation que les ingénieurs ont jugé suffisant pour le vulgaire ne l'est pas pour mes oreilles d'or.

Ce qu'en disent les maths:
--------------------------
le théorème de l'échantillonnage apporte une preuve mathématique que, lorsque la fréquence d'échantillonage devient strictement supérieure à deux fois la fréquence maximale contenue dans le signal (condition du critère d'échantillonnage):
1) Les échantillons contiennent la totalité de l'information du signal continu d'origine. En supprimant ce dernier et en ne conservant que les échantillons, on ne perd donc absolument aucune information.
2) A partir des seuls échantillons, on peut reconstruire exactement le signal continu d'origine, donc tout ce qu'il y avait entre les échantillons. Il faut insister sur le mot "exactement": ce n'est pas une approximation.
3) Non, on ne peut pas relier les pointillés d'une manière différente, le critère d'échantillonnage garantit justement une reconstruction unique et sans ambigüité.
4) Et de toutes façons non, la reconstruction ne se fait pas en "reliant les pointillés", c'est un peu plus compliqué que ça.

En adossant une action de reconstruction à une action d'échantillonnage, on obtient donc au total une opération transparente, le signal continu à l'entrée se retrouve tel quel à la sortie, comme s'il ne s'était rien passé.

L'intuition crie que ce n'est pas possible, mais l'intuition a tort, et les maths ont raison.

La théorie de l'échantillonnage est d'application beaucoup plus large que l'audio numérique, mais pour le son, considéré comme limité à 20 kHz, une fréquence d'échantillonnage juste supérieure à 40 kHz permettra de capturer toute l'information sonore. 40001 Hz convient, par exemple. Il n'y a pas de meilleure approximation en augmentant puisque, dés ce stade, il n'y a plus d'approximation du tout.

Pour des questions de réalisation pratique, il convient toutefois de se donner une marge raisonnable, en particulier pour limiter les contraintes sur les filtres analogiques obligatoirement présents à l'entrée et à la sortie de la chaine audionumérique. On trouve ainsi 44,1 kHz pour le CD, 48 kHz pour les DVD, et sur fichiers dématérialisé, on peut atteindre 192 kHz, ce qui permettrait de reproduire les ultrasons jusque dans les 90 kHz, pour ceux qui y tiennent vraiment, et qui seraient équipés de haut-parleurs et d'oreilles très spéciaux (si on s'appelle Batman, peut-être), sans parler des micros à l'enregistrement.

Je pense que la faute originelle de l'intuition est de croire que, sous prétexte qu'une courbe continue contient une infinité de points, elle contient forcément aussi une infinité d'information, mais c'est tout simplement faux. La contrainte d'une bande passante finie limite la vitesse et donc la granularité d'évolution "horizontale", le long de l'axe du temps, et le rapport signal/bruit limite la finesse des informations "verticales" d'amplitude en les noyant dans le bruit. Il en résulte le thèorème de Shannon sur la capacité d'un canal, qui permet de calculer directement le débit d'information maximal (exprimé en bits/s) transmissible sans erreur à partir de la bande passante et du rapport signal/bruit. La chaine audionumérique qui part du micro pour aboutir au haut parleur de l'auditeur final, via support de stockage intermédiaire, peut-être vue comme un tel canal. Le fait d'utiliser des bits/s n'exclut pas l'analogique de cette limitation, c'est juste une unité de mesure. On peut donc capturer cette information finie avec un nombre d'échantillons fini.

Le rapport signal/bruit n'est pas pris en compte comme limitation dans le théorème de l'échantillonnage, car les échantillons ont une amplitude analogique qui peut varier de façon continue. Si on a un signal théorique sans aucun bruit donc avec une information verticale infinie, l'échantillon peut capturer cette information en prenant une amplitude infiniment précise également.

[gammaburst]

1.2) La reconstruction:
==============

Préliminaire sur une notion de base de traitement du signal: Au lieu de considérer l'évolution de l'amplitude du son en fonction du temps, On peut s'intéresser aux fréquences qu'il contient, donc à la puissance émise en fonction de la fréquence. On pourrait penser qu'en faisant cela on extrait l'information de fréquence et on laisse le reste, mais il n'y a pas de reste. La courbe en fréquence contient toute l'information du signal au même titre que la représentation temporelle. C'est juste le même signal vu sous 2 angles différents. La preuve en est que l'on peut passer du signal temporel au signal fréquentiel en appliquant une transformée de Fourier. Mais on peut aussi passer du fréquentiel au temporel par une transformée de Fourier inverse et on retrouve le signal temporel de départ sans avoir rien perdu (en toute rigueur la courbe fréquentielle est aussi accompagnée d'une courbe de phase). Ce qu'il faut retenir de tout cela, c'est que c'est le même signal des deux côtés, et que selon ce qui est le plus commode, on peut raisoner en fréquentiel ou en temporel, et les conclusions obtenues s'appliqueront aux deux.

A quoi ressemble notre signal échantillonné (en "pointillé") dans le domaine fréquentiel (dit aussi domaine spectral)? Une des démontrations du théorème révèle que, bien loin d'avoir perdu de l'information, on l'a au contraire répliquée à l'infini.
Le signal de départ était un spectre (courbe en fréquence) unique, symétrique, centré sur 0 kHz, allant de -20 kHz à +20 kHz (je passe sur la signification philosophique des fréquences négatives, disons que c'est un sous-produit de l'outil mathématique utilisé, la tranformée de Fourier). Après échantillonnage, on retrouve, en plus de l'original, une copie exacte centrée sur la fréquence d'échantillonnage, par exemple 44.1 kHz, une autre centrée sur 88.2 kHz et ainsi de suite tous les 44.1 kHz, et pareil du côté négatif. Le critère d'échantillonnage garantit que ces spectres ne se télescopent pas, ce qui corromprait les fréquences dans les zones de chevauchement.



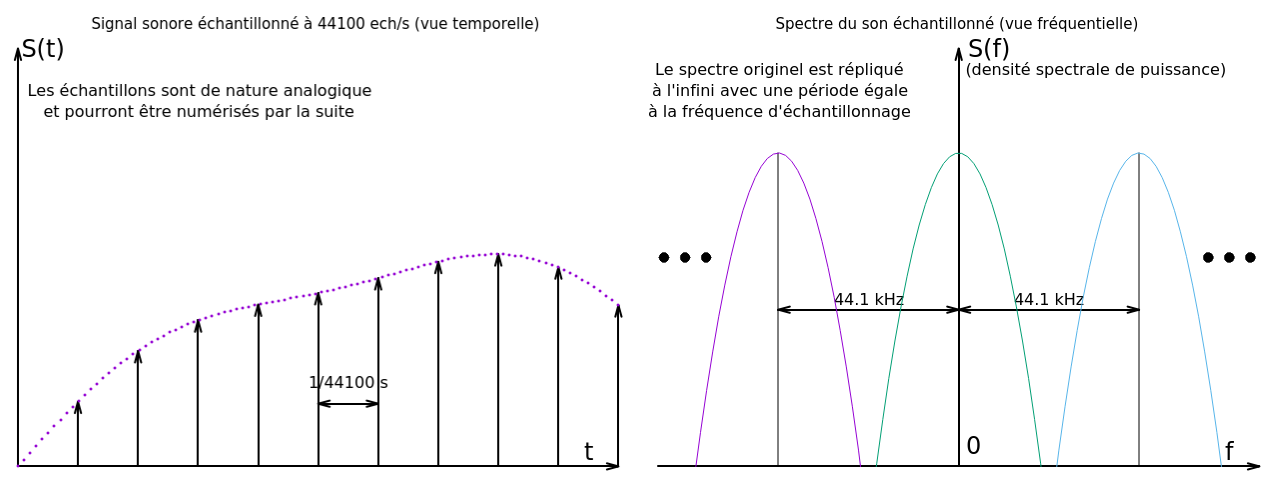
Un signal échantillonné, c'est ça, vu dans le domaine spectral. Comment je retrouve mon signal de départ ? Eh bien il suffit d'isoler mon spectre unique original centré sur zéro donc d'éliminer tous les autres situés dans les fréquences plus élevées qui ont été rajoutés par l'échantillonnage, et pour cela on peut se contenter d'un "simple" filtre passe-bas centré sur zéro, et coupant juste au delà de +/- 20 kHz. Ce filtre situé à la fin de la chaine échantillonnée est pour cela appelé filtre de reconstruction.

Problème, il faut appliquer le filtre sur le signal echantillonné, qui est un concept abstrait dans lequel chaque échantillon est une impulsion de puissance infinie, de durée infiniment courte, contenant au total une énergie finie et bien déterminée correspondant à la valeur de mesure de l'échantillon. Ce signal n'est guère réalisable en pratique. Par contre, on peut imaginer qu'on lui applique ce qu'on appelle un "bloqueur d'ordre zéro", qui a simplement pour effet de maintenir le signal à la valeur de l'echantillon pendant une période d'échantillonnage, puis la valeur de l'échantillon suivant pendant la période suivante, et ainsi de suite, cela donne une suite d'impulsions rectangulaires jointives, donc le fameux signal en marches d'escalier si injustement décrié. Ce signal échantillonné-bloqué est très facile à produire électroniquement, il suffit de maintenir la sortie du convertisseur numérique analogique constante à la valeur de mesure (finie) pendant une période d'échantillonnage à chaque conversion.

Quel est l'effet du bloqueur d'ordre zéro dans le domaine spectral? On montre que le spectre échantillonné (donc la suite infinie de spectres répliqués) se retrouve multiplié par un sin(x)/x (sinus cardinal=sinc) centré sur le 0. il y a donc un gros lobe central qui retombe à zéro à la fréquence d'échantillonnage par exemple 44.1 kHz, un plus petit lobe entre 44.1 et 88.2, et ainsi, de suite avec une baisse d'amplitude moyenne en 1/x. Il y a donc déjà une action d'atténuation des hautes fréquences qui, bien qu'imparfaite, va venir renforcer l'action du filtre de reconstruction qui arrive après.



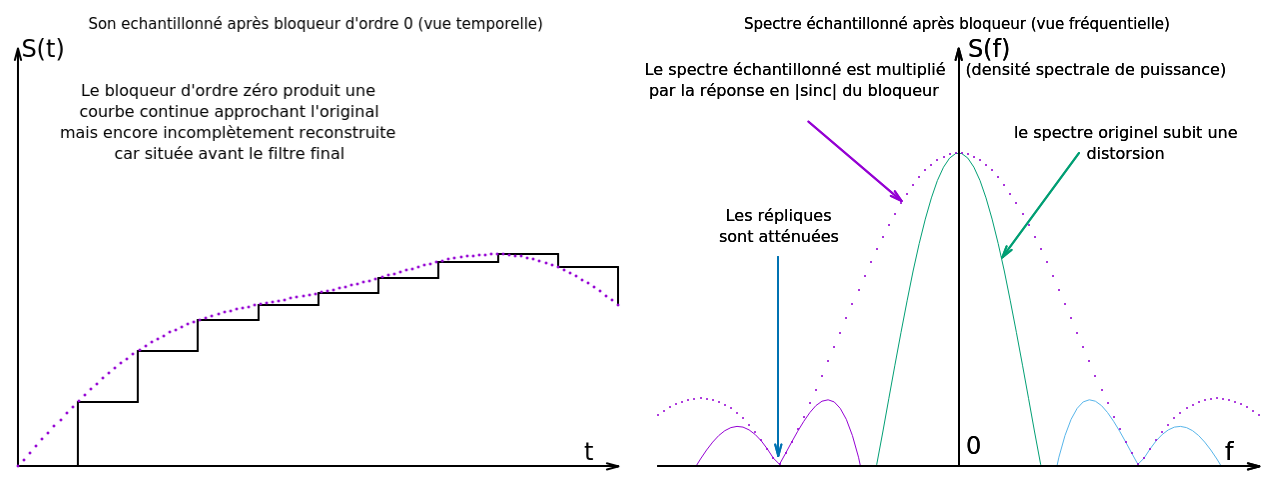
Les fréquences utiles entre -20 kHz et + 20 kHz sont entièrement sous le premier lobe, bien avant le premier zéro. Elles sont donc préservées, mais on calcule que du fait de la courbe en sinus cardinal, elle subissent une distorsion, avec une atténuation jusqu'à 4 dB pour la fréquence utile la plus élevée. Une distorsion n'est pas une perte d'information, juste une déformation, que l'on peut inverser si on la connait. Puisqu'on part du domaine numérique, on peut y appliquer un filtre numérique de précompensation, qui va permettre d'annuler cet effet, et au total de retrouver ainsi exactement le signal de départ, après application du filtre de reconstruction analogique final. Donc, effet du bloqueur et des marches d'escalier: même pas mal !

On voit ainsi que, par exemple, la fréquence la plus élevée à 20 kHz n'a pas du tout été massacrée par le bloqueur, juste atténuée de 4 dB, atténuation qui a été déjà précompensée avant le convertisseur. Elle n'a pas non plus été abimée par le fait de n'avoir que 2 + epsilon échantillons par période, car le critère d'échantillonnage a été respecté.

Il faut ajouter que cette vision du convertisseur produisant directement une tension bloquée correspondant à la valeur de l'échantillon pendant une période est un peu ancienne, de nos jours ils sont plutôt basés sur un coeur delta-sigma (dit "one bit") qui va produire des créneaux d'amplitude constante à très haute fréquence dont le filtre passe-bas prendra la valeur moyenne.

Tout ce qui vient d'être dit est essentiellement centré sur la théorie de l'échantillonnage qui si vous vous rappellez, est de nature analogique. On n'est donc pas encore entré dans le monde numérique.

[gammaburst]

2) Numérisation:
==============
Pour cela, il faut numériser les échantillons au moyen d'un convertisseur analogique numérique. Celui-ci va au final produire une valeur numérique exprimée sur 16 bits dans le cas du CD (j'exclus de cette explication les systèmes SACD/bit stream). 16 bits peuvent encoder 65536 valeurs différentes, à partager entre les parties positives et negatives donc l'amplitude est codable sur 32767 niveaux discrets. Le signal analogique peut tomber n'importe où entre deux niveaux, il y a donc une erreur de mesure, maximale si le signal tombe à mi-chemin entre deux paliers, donc égale à un demi LSB (Least Significant Bit ou bit de poids le plus faible). Il est mathématiquement équivalent de considérer que l'on a effectivement réussi une conversion parfaite, de précision infinie, mais que l'on a ensuite surimposé au résultat un bruit d'amplitude crête égale à un demi LSB. Le fait de ne plus avoir une précision infinie dans les échantillons introduit donc tout simplement un plancher de bruit. Le rapport signal/bruit correspondant à 16 bits peut être calculé et donne environ 96 dB.

Cette valeur est au moins de 26 dB meilleure que pour les supports analogiques, néanmoins contrairement à eux ce bruit n'est pas entièrement aléatoire, il a un certain degré de corrélation avec le signal et cela peut dans certaines circonstances créer une gêne. On a résolu ce problème en rajoutant un peu de bruit aléatoire (2 à 3 dB) permettant de décorreler le bruit de quantification du signal. Voir à cet égard la démonstration de Monty (https://www.youtube.com/watch?v=UqiBJbREUgU).
Cette pratique s'appelle le "dithering" et, bien maitrisée, elle permet de faire des choses magiques, comme encoder une dynamique de 110 dB, soit un signal à 110 dB en dessous du 0 dBFS (pleine échelle numérique), malgré le SNR limité à 96 dB.
Entre autres raisons, il faut noter que les 96 dB correspondent au bruit récupéré sur toute la bande passante de 20 à 20 kHz, un signal qui serait défini sur une bande passante plus étroite récupérera un niveau de bruit plus faible.

Une conclusion possible est que oui, une chaine numérique perd de l'information, mais pas plus qu'une chaine analogique de même spécifications en bande passante et rapport signal/bruit, et les pertes se font pour les mêmes causes: limitation de la bande passante, qui fait perdre les ultrasons (pour le CD standard), et rapport signal bruit, qui fait perdre les informations d'amplitude les plus fines.
Le fait de rajouter une étape d'échantillonnage n'apporte aucune perte nouvelle, c'est transparent. Et comme les spécifications du numérique en rapport signal/bruit sont hors de portée des supports analogiques, ce sont au final ces derniers qui perdent le plus d'information.

[gammaburst]

Tout ceci est axé sur la théorie de base qui est nécessaire pour comprendre le véritable mécanisme sous -jacent qui est à l'oeuvre. Il y a un deuxième niveau de jeu en passant à la réalisation physique, ce sera pour un futur épisode.

[yoyoman]

Clair net et précis.
Merci pour ces explications vulgarisés (à prendre dans le bon sens du terme)