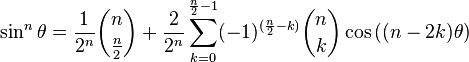|
|
Modérateurs: Modération Forum Installations, Modération Forum DIY, Le Bureau de l’Association HCFR • Utilisateurs parcourant ce forum: Delaforetnoire, tracerbox et 80 invités
Discussions générales sur le DIY Audio : choix des HP, comparaisons des principes : clos vs BR, etc
mini quiz pic de fractionnement membrane rigide
Sauvés !
- Kro
- Messages: 29438
- Inscription Forum: 12 Jan 2004 19:24
- Localisation: Isère (38)
FIN DU SUJET !
Merci à tous de votre contribution.
Pas de sous-harmoniques ni de fondamentales distordues mais une simple représentation du niveau de distorsion des harmoniques sur leurs fondamentales.
C'est maintenant clair pour tout le monde (enfin j'espère)
Merci à tous de votre contribution.
Pas de sous-harmoniques ni de fondamentales distordues mais une simple représentation du niveau de distorsion des harmoniques sur leurs fondamentales.
C'est maintenant clair pour tout le monde (enfin j'espère)
La configuration dans mon profil
Un bon son, c'est quand ça sonne naturel, point. Et tout le monde est capable de le reconnaître, pas de soucis.
-

Agnostic1er - Superviseur Forum DIY

- Messages: 11607
- Inscription Forum: 19 Oct 2005 3:26
- Localisation: Corrèze, à 500m de la Dordogne
ah non, y a encore le quiz de tcli sur l'ordre nombre entier des H et pourquoi pas à des fr inférieures...
La configuration dans mon profil
Un bon son, c'est quand ça sonne naturel, point. Et tout le monde est capable de le reconnaître, pas de soucis.
-

Agnostic1er - Superviseur Forum DIY

- Messages: 11607
- Inscription Forum: 19 Oct 2005 3:26
- Localisation: Corrèze, à 500m de la Dordogne
Je me lance mais je vous le dis je vais atteindre le ridicule. Dans un système périodique une fréquence donnée peut être décomposée en une somme de fréquences, toutes multiples. La fréquence la plus basse est la fondamentale et les autres sont appelées harmoniques. On doit les retrouver grâce aux série de fourier (un auxerrois  ) mais là je nage en pleine brume
) mais là je nage en pleine brume 
- Kro
- Messages: 29438
- Inscription Forum: 12 Jan 2004 19:24
- Localisation: Isère (38)
Kro a écrit: fourier (un auxerrois)
2 points en plus sur ta copie

- androuski
- Messages: 23171
- Inscription Forum: 14 Mar 2007 14:43
- Localisation: C'est un trou, mais rempli de pinard, donc ça me va.
Kro a écrit:Je me lance mais je vous le dis je vais atteindre le ridicule. Dans un système périodique une fréquence donnée peut être décomposée en une somme de fréquences, toutes multiples. La fréquence la plus basse est la fondamentale et les autres sont appelées harmoniques. On doit les retrouver grâce aux série de fourier (un auxerrois) mais là je nage en pleine brume
Oui.
On envoie un signal électrique sinusoidal (donc périodique) de fréquence f au haut parleur (signal d'entrée). Avec un micro, on mesure la pression acoustique générée par la membrane en mouvement (signal de sortie). Si le haut parleur était parfait, on mesurerait une parfaite sinusoide, comme pour le signal d'entrée. Or le haut parleur (imparfait) distord le signal de sortie. C'est à dire qu'au lieu d'être une sinusoide parfaite, c'est une sinusoide déformée. MAIS de fréquence tjrs égale à f (fréquence du signal d'entrée).
sinusoide de fréquence f ----> haut parleur ----> signal de fréquence f, ressemblant à une sinusoide mais déformée
La question à laquelle on a besoin de répondre alors, c'est : "de combien est distordu mon signal". On a besoin de quantifier la déformation engendrée par le haut parleur. Or cela est difficile à réaliser seulement par l' "observation" de la sinusoide déformée.
C'est pourquoi on effectue une transformée de fourier du signal de sortie. On passe alors du domaine temporel "tension=fonction(temps)" au domaine fréquentiel "amplidude=fonction(fréquence)". Et là fourier nous dit (en gros) que toute fonction continue périodique (notre signal de sortie) est décomposable en une série de fourier, composée d'une fondamentale (de fréquence f comme notre signal d'entrée) à laquelle s'ajoutent des harmoniques dont les fréquences sont égales à des multiples entiers de la fréquence fondamentale (2f, 3f, 4f et ainsi de suite). La fondamentale est la composante "pure" (zéro disto), les harmoniques sont dues au déformations du haut parleur. Et permettent de quantifier la déformation qu'il génère. On obtient donc une série de raies, dont on visualise facilement l'amplitude. Si la raie à 2f est élevée, on dit que H2 est élevée. C'est mieux que de regarder la sinusoide deformée et dire, "mon dieu que cette sinusoide est déformée !" .
(Y a des explications sur internet bien meilleures que ça !)
Le problème est que c'est une représentation théorique (transformée mathématique). Ca permet de dire si la distorsion était importante ou non. Mais ne permet aucunement de dire comment elle sera percue par l'oreille. Certaines "tronches" de l'audio disent que c'est une représentation qui n'a aucune valeur sur un plan psychoacoustique, et ne permet absolument pas de présager de la qualité sonore d'un hp.
http://www.diyaudio.com/forums/multi-wa ... ption.html
- gbadaut
- Messages: 403
- Inscription Forum: 02 Aoû 2009 0:51
- Localisation: Lyon
gbadaut a écrit:On envoie un signal électrique sinusoidal (donc périodique) de fréquence f au haut parleur (signal d'entrée). Avec un micro, on mesure la pression acoustique générée par la membrane en mouvement (signal de sortie). Si le haut parleur était parfait, on mesurerait une parfaite sinusoide, comme pour le signal d'entrée. Or le haut parleur (imparfait) distord le signal de sortie. C'est à dire qu'au lieu d'être une sinusoide parfaite, c'est une sinusoide déformée. MAIS de fréquence tjrs égale à f (fréquence du signal d'entrée).
Effectivement, mais pourquoi ?
A partir du moment où on passe dans une fonction non linéaire qui déforme le signal , quelle garantie que le signal est toujours à la même fréquence ?
- tcli
- Messages: 4075
- Inscription Forum: 23 Nov 2009 22:40
- Localisation: Complètement à l'ouest
Du coup j'ai joué avec google. Pour représenter ce que dit gbadaut :

Sur b on voit la sinusoide déformée. Sur a on voit la décomposition de la fondamentale +H3. F+H3 = la sinusoide déformée.

Sur b on voit la sinusoide déformée. Sur a on voit la décomposition de la fondamentale +H3. F+H3 = la sinusoide déformée.
- Kro
- Messages: 29438
- Inscription Forum: 12 Jan 2004 19:24
- Localisation: Isère (38)
tcli a écrit:gbadaut a écrit:On envoie un signal électrique sinusoidal (donc périodique) de fréquence f au haut parleur (signal d'entrée). Avec un micro, on mesure la pression acoustique générée par la membrane en mouvement (signal de sortie). Si le haut parleur était parfait, on mesurerait une parfaite sinusoide, comme pour le signal d'entrée. Or le haut parleur (imparfait) distord le signal de sortie. C'est à dire qu'au lieu d'être une sinusoide parfaite, c'est une sinusoide déformée. MAIS de fréquence tjrs égale à f (fréquence du signal d'entrée).
Effectivement, mais pourquoi ?
A partir du moment où on passe dans une fonction non linéaire qui déforme le signal , quelle garantie que le signal est toujours à la même fréquence ?
Explication "avec les mains" : Pcq l'impulsion électrique impose "son rythme" à la réponse mécanique.
- Kro
- Messages: 29438
- Inscription Forum: 12 Jan 2004 19:24
- Localisation: Isère (38)
Pour la distorsion harmonique et l'intermodulation; j'ai créé un sujet ici.
viewtopic.php?f=1&t=29973236
Après, on pourra y parler de la perception ....
viewtopic.php?f=1&t=29973236
Après, on pourra y parler de la perception ....
- JIM
- Modérateur Installations

- Messages: 7084
- Inscription Forum: 19 Nov 2001 2:00
- Localisation: Toulouse
La perception on entre dans le subjectif et pour moi c'est bien plus problèmatique et on pourrait en parler des heures.
- Kro
- Messages: 29438
- Inscription Forum: 12 Jan 2004 19:24
- Localisation: Isère (38)
tcli a écrit:gbadaut a écrit:On envoie un signal électrique sinusoidal (donc périodique) de fréquence f au haut parleur (signal d'entrée). Avec un micro, on mesure la pression acoustique générée par la membrane en mouvement (signal de sortie). Si le haut parleur était parfait, on mesurerait une parfaite sinusoide, comme pour le signal d'entrée. Or le haut parleur (imparfait) distord le signal de sortie. C'est à dire qu'au lieu d'être une sinusoide parfaite, c'est une sinusoide déformée. MAIS de fréquence tjrs égale à f (fréquence du signal d'entrée).
Effectivement, mais pourquoi ?
A partir du moment où on passe dans une fonction non linéaire qui déforme le signal , quelle garantie que le signal est toujours à la même fréquence ?
Bonne question. Je n'ai pas la réponse.
- gbadaut
- Messages: 403
- Inscription Forum: 02 Aoû 2009 0:51
- Localisation: Lyon
Kro a écrit:Dans un système périodique une fréquence donnée (un signal périodique) peut être décomposée en une somme de fréquences, toutes multiples. La fréquence la plus basse est la fondamentale et les autres sont appelées harmoniques. On doit les retrouver grâce aux série de fourier (un auxerrois)
Oui mais qu'est ce qui se passe quand on passe tout ça dans une fonction non linéaire ?
Bon , va y avoir un peu de math

Mathématiquement, la valeur d'un signal sinusoïdal de fréquence f en fonction du temps t se note sin(w.t) (avec w=2.pi.f) .
Que va devenir ce signal si on le passe à travers une fonction F non linéaire comme par exemple :
 [/URL]
[/URL]Cet exemple est un cas de fonction non linéaire assez classique : pour des valeurs d'entrés faibles la sortie est quasi linéaire (droite a l'origine), mais pour de plus grandes valeurs, on atteint la limite du système et ça sature .
L'ennui, c'est qu'en pratique, cette fonction peut prendre à priori n'importe quelle forme , donc si on veut mettre tout ça en équation , il va falloir modéliser cette fonction F.
Il y a un outil pratique pour ça : les fonctions polynomiales. Ce sont des fonctions du genre a0+a1.x+a2.x²+a3.x³+.....an.xn
Le truc bien, c'est que si F n'est pas trop tordue, on peut toujours trouver un jeu de coef ai qui vont approximer F à n'importe quelle précision voulue.
Il suffit de prendre n suffisamment grand et de chercher les coefs ai (y a des méthodes automatiques).
Par exemple, la fonction F du graphe ci-dessus est égale à x-1/3.x³
Bien , maintenant que l'on a une équation pour F , que ce passe t'il quand on lui envoie en entré un signal sinusoïdal ?
Il suffit de remplacer les x dans notre polynôme par des sin(w.t), ça donne :
a0+a1.sin(w.t)+a2.sin(w.t)²+a3.sin(w.t)³+......an.sin(w.t)n
Bon, on est pas plus avancé... sauf que :
Si on regarde les égalités trigonométriques, on s’aperçoit que :
sin(w.t)²= 1/2-1/2.sin(2.w+pi/2) et que sin³=3/4.sin(w.t)-1/4.sin(3.w.t)
hum, hum, il semble qu'un sinus élevé à une puissance soit égale à une somme de sinus de fréquence multiple (2.w=2.pi.2f)
Ben voila, on les a nos harmoniques !!!!
En fait il y a une formule plus générale , valable pour toute valeur de n ( en texte caché pour les âmes sensibles) :
Spoiler : cliquer pour lire
Peut importe, la formule, ce qui est important c'est qu'elle indique que tout sinus élevé à une puissance est égale à une somme de sinus (ou cos c'est la même chose à un déphasage de pi/2 près) à des fréquences multiples (le (n-2k) dans la formule) .
Pas de composantes à des fréquences 1/2 ou 2.5 ou je ne sais quoi !, que des multiples entier de la fréquence d'entrée !
CQFD
Il y a un autre truc important que dit cette formule barbare, c'est que pour des puissances paires (2,4,6...) , on aura une somme de sinus à des fréquences multiples paires (réciproquement pour des puissances impaires) .
Or, les polynômes ont une propriété intéressante :
si un polynôme n'est constitué que de puissances impaires (et que ao=0) alors il est symétrique par rapport à l'origine ( f(-x)=-f(x))
Donc quand on a une fonction non linéaire à peu près symétrique, elle générera essentiellement des harmoniques impaires.
C'est le cas d'un étage de sortie push-pull d'un ampli.
Au contraire, si la non linéarité est dissymétrique, elle produira des harmoniques paires . Comme par exemple un étage de sortie SE d'un ampli classe A.
Étonnant non ?
PS : et le rapport avec Rennes ?
Il semblerait que la formule barbare ci-dessus (ou son inverse) ai été découverte au 16eme siècle par un type étonnant : François Viète, qui fut entre beaucoup d'autres choses, député au parlement de Bretagne à Rennes ....
Dernière édition par tcli le 01 Oct 2011 0:08, édité 1 fois.
- tcli
- Messages: 4075
- Inscription Forum: 23 Nov 2009 22:40
- Localisation: Complètement à l'ouest
Merci d'avoir pris soin d'expliquer tout ça tcli!...surtout pour les matheux parce que les autres...enfin t'y es pour rien hein, la science elle est comme ça...
androus, capito?
androus, capito?
La configuration dans mon profil
Un bon son, c'est quand ça sonne naturel, point. Et tout le monde est capable de le reconnaître, pas de soucis.
-

Agnostic1er - Superviseur Forum DIY

- Messages: 11607
- Inscription Forum: 19 Oct 2005 3:26
- Localisation: Corrèze, à 500m de la Dordogne
Agnostic1er a écrit:Merci d'avoir pris soin d'expliquer tout ça tcli!...surtout pour les matheux parce que les autres...
Et encore, si j'avais parlé d'intermodulation ça aurait été pire
L'intermodulation ,c'est quand on considère , non pas un mais plusieurs (par exemple 2 : f1 et f2 ) signaux sinusoïdaux en entré d'une fonction non linéaire.
Je passe sur les calculs (car là ça devient un peu compliqué
aussi tous un tas d'autres signaux aux fréquences +/-a.f1+/-b.f2. (a et b étant des coef entiers encore une fois).
Le truc amusant c'est les - :
Ainsi si tu as du 250Hz et 200Hz en entré , tu pourras avoir en sortie du 250-200=50Hz !!!!, mais aussi du 2.250-200=300Hz et ainsi de suite
Heureusement, plus a et b sont grand plus l'amplitude du signal sera faible, mais quand même quelle soupe de fréquence , et dire qu'on écoute ça
A moins , que comme le disait gbadaut , que ça n'ait pas trop d'importance et que ce qui compte c'est la façon dont on perçoit le tout .
- tcli
- Messages: 4075
- Inscription Forum: 23 Nov 2009 22:40
- Localisation: Complètement à l'ouest
|
Retourner vers Discussions Générales
|