J'imagine que l'on mixe aussi les technos et longueurs d'ondes (en dehors du spectre visible, j'entends)
petit MP pour ne pas "polluer" le post, si tu préfères
|
|
Modérateurs: Modération Forum Haute-Fidélité, Le Bureau de l’Association HCFR • Utilisateurs parcourant ce forum: Aucun utilisateur enregistré et 23 invités
Emile écrit : exemple type HOVLAND HP100 qui utilise le top en composants internes (on est fournisseur ou on ne l'est pas héhéhé)
et des tubes Sovtek, décriés sur les Audio Research et là on oublie ?! !
Emile a écrit:Monsieur
Ce sont des condos à base d'huile d'olive bio premier pressage à froid !
haskil a écrit:Mais bon, j'écoute vraiment beaucoup de musique...
Abraham.ctl a écrit:si l'on souhaite reconstituer un bruit de Poisson (évènements ponctuels arrivant à des moments régis par une certaine loi de probabilité)à l'aide d'une sinusoïde, le résultat ne sera pas très bon. Or, la musique, c'est un mix entre des sinusoïdes et des attaques. Or, la survenance des attaques ne peut être connu à l'avance et n'est pas codé par l'échantilloneur dont la fréquence est fixe, d'où l'intérêt (le message sinusoïdal) et la limite (le attaques) du suréchantillonage.
Abraham.ctl a écrit:le temps infini n'est pas seulement nécessaire pour calculer les oscillations basse fréquence, mais aussi pour calculer les oscillations hautes fréquences très proches de Fe/2.
Imagine que l'amplitude soit très forte (1000) que se passe-t-il dans la pratique si par hasard l'échantillonage commence sur le passage au neutre. Et bien , le convertisseur sortira 0 puis 0.1 puis 0.5 puis 1 puis 1.7 puis ... et il faudra une très longue période de temps pour arriver à 1000. Donc le DAC aura transformé une oscillation très haute fréquence (proche de Fe/2) en oscillation très basse fréquence. Du grand n'importe quoi.
D'où l'utilité d'augmenter la fréquence d'échantillonage par rapport à la fréquence max que l'on veut reproduire. 10 points pour reproduire correctement une sinusoïde, ce n'est pas du luxe (prendre une feuille de papier et un crayon pour s'en convaincre). Dans ce cas, le temps d'échantillonage n'a plus besoin d'être infini, mais il est tout de même de 10/Fe pour avoir une oscillation à Fmax (ce qui est finalement une application pratique de l'infini).
Xéna a écrit:Mais ce qui est important, c'est que dire qu'à 44.1KHz on reproduit correctement le 20kHz est une vue de l'esprit.
haskil a écrit:Ce qui, du reste, a été montré plusieurs fois sur le forum. Alors, comme tu le dis si bien : on se répète.
Pio2001 a écrit:Si on enregistre du 20 kHz, la quantification s'annulle tous les 11 échantillons à peu près. Si le filtre interpolateur/passe-bas/antialias prend en compte plus de 11 échantillons à la fois pour ses calculs, le 20 kHz sera rétabli de façon parfaitement continue à partir des échantillons qui oscillent.




antonyantony a écrit:Alain,
Je crois que parfois, on confond musicalite ( = j aime le son) et fidelite (= proche de l original).

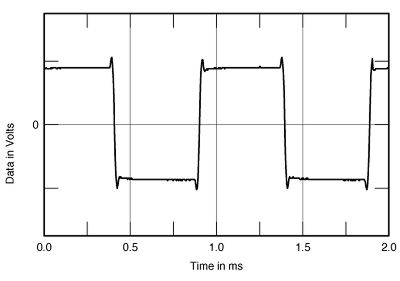
antonyantony a écrit:Il y a qq chose qui s oppose a la restitution du signal sans distorsion :
C est le principe d incertitude d heisenberg. Ce que le filtre gagne en precision temporelle il le perd en precision frequentielle.
antonyantony a écrit:On a doonc bien une forme de distorsion induite par le filtre.
antonyantony a écrit:Rappelons aussi que la transformee de fourier ne peu s appliquer qu a des fonctions periodiques. Ce qui veut que c est une fonction globale et non locale. Ce qui implique qu une transformee de fourier fit perdre toute reference temporelle.
|
Retourner vers Lecteurs CD & SACD |