Comprendre les mystères du rendement HP VS compression

[androuski]

Ah,
Jean a dit la même chose en mieux et plus rapidement

[Invite107]

J'ai repris les équations de propagations d'onde dans un pavillon pour calculer le profil de la pression et de la vitesse. Rappelons dans un premier temps les relations entre puissance sonore, intensité, pression et vitesse. Nous avons :

L'intensité est la puissance divisée par la surface. La puissance est la force multiplié par la vitesse. On déduit que l'intensité est la pression multiplié par la vitesse.

On définit l'impédance acoustique par le quotient de la pression sur le débit. Le débit est la surface multiplié par la vitesse. On déduit que la puissance est l'impédance multiplié par le carré du débit.

L'impédance acoustique dans un pavillon à une section d'abscisse x est complexe a calculer. Mais on peut simplifier en faisant l'hypothèse d'un pavillon infini dans lequel seule une onde progressive se déplace et en se plaçant à une fréquence bien supérieure à la fréquence de coupure.

Dans ces conditions l'expression de l'impédance est :

L'impédance est le quotient de l'impédance spécifique de l'air (ρ C) divisé par la surface de la section. L'impédance augmente de la bouche à la gorge : c'est l'adaptation d'impédance, avantage que procure le pavillon.

A partir de l'impédance on peut calculer la puissance acoustique à l'abscisse x. On trouve :

Cette puissance étant constante (conservation de l'énergie) on peut calculer la vitesse et la pression à l'abscisse x. On obtient :

Le rapport entre la pression et la vitesse vaut l'impédance spécifique comme dans le cas des ondes planes. La pression et la vitesse augmente de la bouche à la gorge et varie comme l'inverse de la racine carré de la surface de la section.

Je m'étais un peu mélangé les pinceaux hier ...

[Invite107]

La même chose que ce que je disais plus haut avec les 98/2 et 90/10. La même quantité de pertes coté électrique (valeur absolue) représente une proportion variable des pertes globales réparties entre pertes électriques et "pertes" acoustiques (celles qu'on veut voir augmenter).

Parce que sinon je ne vois vraiment pas où tu coinces, devant un fait qui semble quand même bien établi et de façon consensuelle.

Bonjour Androuski,

Dans ce cas c'est que tu n'as pas compris la notion de rendement, je pense.

Cette remarque ne manque pas de piquant car androuski a parfaitement compris la notion de rendement puisque c'est justement la répartition dont il parle qui varie et qui explique que le rendement augmente

J'aimerai savoir quel serait le rendement d'un HP à radiation directe dont les paramètres seraient les suivant :

- BL = 15 Tm
- SD = 40 cm²
- Re = 5 Ohms
- MMS = 1 Gr

Est-il possible d'avoir une réponse à cette question ?

Je vais essayer de calculer le vrai rendement (true efficiency). Comme je l'ai indiqué, le calcul du rendement du HP (formule de votre premier post) est valable dans le cas ou la résistance de rayonnement est négligeable. De plus il s'agit d'un rendement nominal (nominal efficiency) dans lequel on ne calcule pas la puissance totale mais seulement la puissance débité dans la résistance du HP. Pour le calcul du vrai rendement il faut donc prendre en compte Rms.

[Invite107]

Le rendement d'un HP est le rapport entre la puissance acoustique et la puissance totale. Le HP est le siège de deux transformation : une transformation électrique vers mécanique et mécanique vers acoustique. Voir ce schéma :

On considère généralement que le transfert mécanique acoustique est adiabatique, ce qui signifie qu'il n'y a pas de création de chaleur. Dans ces conditions le rendement mécanique acoustique vaut 1 et le rendement du HP se réduit au rendement entre la partie électrique et mécanique.

Dans le schéma on voit bien les éléments de pertes. Ce sont du coté électrique Re et Revc, du coté mécanique Rm. Du coté acoustique ra est la transformation acoustique. Il n'y a pas de résistance supplémentaire qui prendrait en compte un effet thermique.

[Esscobar]

Oui, sauf que Jean écrit aussi ceci : post180753916.html#p180753916


Ce qui contredit la capture que tu as mise, qui stipule que S1 x V1 = S2 x V2 ... Alors que Jean dit que S1 x V1 < S2 x V2.

Je voulais parler de la vitesse des molécules d'air à l'entrée de la chambre de compression. On a Sd x Vd = Sg x Vg et donc Vd<Vg puisque Sd > Sg.

Mais attention, la relation S1 x V1 = S2 x V2 ne s'applique pas à un pavillon. Cette équation qui est celle de conservation de la masse s'applique dans le cas d'un écoulement d'air. Mais il n'y a pas d'écoulement d'air dans un pavillon. Il y a propagation d'une onde sonore.

Évidemment, mais cela est pareil dans la chambre de compression, ce n'est pas une soufflerie, d'ailleurs au lieu de parler de vitesse (car cela peut induire en erreur), il faudrait plutôt parler d'amplitude de vibration . Ce qui se passe dans une chambre de compression est la même chose que dans un pavillon, sauf qu'on le fait à l'envers (sortie plus petit que l'entrée) et avec une pièce de phase pour garder une bonne phase même dans les hautes fréquences afin de ne pas avoir de chute de SPL à cause d'annulation.

Dans un pavillon, comme cela a été dit, la vitesse des molécules d'air à la gorge est supérieure à celle de la bouche.

Nous sommes d'accord, et c'est plutôt logique, puisqu'il ne peut y avoir de création d'énergie conformément à la loi en carré inverse .

https://fr.wikipedia.org/wiki/Loi_en_carr%C3%A9_inverse

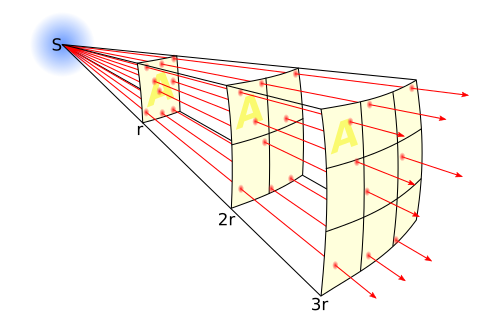
Mais la vitesse de la membrane est inférieure à celle d'un même haut-parleur à radiation directe pour une même puissance acoustique.

Oui

C'est cette propriété qui fait que le rendement augmente parce que les pertes dans le HP diminue puisque le débit diminue.

Ceci ne peut être vrai que si l'intensité acoustique totale est supérieur ... Hors l'énergie hors axe sera plus importante sur le HP à radiation directe que sur le pavillon. Donc le rendement ne change pas contrairement à l'intensité acoustique pour une surface qui privilégie l'avantage en directivité du pavillon.

https://fr.wikipedia.org/wiki/Intensit%C3%A9_acoustique



Ou P est la puissance acoustique en watt et r le rayon de la sphère

L’intensité acoustique est la puissance transportée par les ondes sonores, par unité de surface, mesurée perpendiculairement à la direction de ce transfert. Comme les sons se propagent dans un espace à trois dimensions, certains auteurs (Fahy 1995) construisent l'intensité acoustique en un point de l'espace comme un vecteur dont les composantes sont l'intensité acoustique scalaire, définie comme précédemment, mesurée dans la direction de chacun des axes d'un repère.

En physique, la puissance se définit comme la quantité d'énergie par unité de temps fournie par un système. En mécanique, elle est le produit de l'application d'une force par la vitesse du déplacement de l'objet auquel elle s'applique. En acoustique, cette force créée par l'onde sonore s'applique à une unité de surface du front sonore, dont on peut réduire arbitrairement la taille pour décrire un endroit précis du champ sonore.

D'ailleurs ils abordent ce point :

Lorsque les ondes sonores sont guidées par un tuyau rigide, l'énergie sonore injectée à l'une des extrémités du tuyau ne peut pas se disperser, et se retrouve à l'autre extrémité concentrée sur une surface identique.

Ce phénomène est utilisé dans les conduits acoustiques, pour transmettre des ordres à distance (type Chadburn), comme sur un navire dans un environnement bruyant.

C'est également ce phénomène qui est utilisé dans le pavillon acoustique pour transformer l'impédance acoustique entre la haute impédance de la membrane source et la basse impédance de l'air, en conservant constante l'énergie sonore transmise par le cornet.

[Esscobar]

L'intensité est la puissance divisée par la surface. La puissance est la force multiplié par la vitesse. On déduit que l'intensité est la pression multiplié par la vitesse.

Oui

On définit l'impédance acoustique par le quotient de la pression sur le débit. Le débit est la surface multiplié par la vitesse. On déduit que la puissance est l'impédance multiplié par le carré du débit.

Là je n'ai pas compris, la faute m'incombe ...

https://fr.wikipedia.org/wiki/Imp%C3%A9dance_acoustique

Il est tard, j'ai la tête qui vrille ...

[Esscobar]

Le rendement d'un HP est le rapport entre la puissance acoustique et la puissance totale.

Euh, ce n'est pas plutôt le rapport entre la puissance électrique par rapport à la puissance acoustique (ou mécanique vu que c'est lié).

Le HP est le siège de deux transformation : une transformation électrique vers mécanique et mécanique vers acoustique. Voir ce schéma :

On considère généralement que le transfert mécanique acoustique est adiabatique, ce qui signifie qu'il n'y a pas de création de chaleur. Dans ces conditions le rendement mécanique acoustique vaut 1 et le rendement du HP se réduit au rendement entre la partie électrique et mécanique.

Alors là oui à 200%, c'est ce que je dis depuis pas mal de page maintenant .

Dans le schéma on voit bien les éléments de pertes. Ce sont du coté électrique Re et Revc, du coté mécanique Rm. Du coté acoustique ra est la transformation acoustique. Il n'y a pas de résistance supplémentaire qui prendrait en compte un effet thermique.

Voilà, et c'est bien pour cela que sur un HP qui possède un rendement de 2%, c'est dire 98% de perte en quasi-totalité en chaleur, ajouter une chambre de compression ou un pavillon ne changera pas le fait qu'il y a 98% de perte interne dû à la conversion électrique -> mécanique ... Donc on reste avec le 2% en sortie, le but est maintenant d'optimiser au mieux pour exploiter ce qu'il reste .

[Invite107]

On définit l'impédance acoustique par le quotient de la pression sur le débit. Le débit est la surface multiplié par la vitesse. On déduit que la puissance est l'impédance multiplié par le carré du débit.

Là je n'ai pas compris, la faute m'incombe ...

https://fr.wikipedia.org/wiki/Imp%C3%A9dance_acoustique

Il est tard, j'ai la tête qui vrille ...

Mince alors, vous ne comprenez pas ce qu'est une impédance de rayonnement ? Il me semble que depuis 10 pages, c'est le cœur du sujet non ?

[Esscobar]

Mince alors, vous ne comprenez pas ce qu'est une impédance de rayonnement ? Il me semble que depuis 10 pages, c'est le cœur du sujet non ?

Non c'est juste votre manière de l'exprimer que je n'avais pas compris . Et est-ce que impédance acoustique et impédance de rayonnement sont la même chose pour vous ? Car pour moi cela diffère

Une impédance acoustique c'est le rapport entre une pression (Pa) par une vitesse (m/s) (a ne pas confondre avec la célérité du son : 344 m/s).

Imp_Acoust = Pression / Vit_son

Et lorsqu'il s'agit d'une onde acoustique plane progressive :

Imp_acoust = Masse_volumique (du milieu) x Vit_son

Masse volumique (kg/m3), ce qui signifie l'importance du pavillon à ce niveau, car la masse volumique dans le "cône" du pavillon est évidemment plus faible que la masse volumique d'une pièce ou en extérieur . En notons un point important :

Lorsqu'une onde acoustique rencontre l'interface séparant deux milieux d'impédances acoustiques différentes, une partie de l'onde est transmise dans l'autre milieu tandis qu'une autre partie se réfléchit sur l'interface. La notion d'impédance acoustique permet d'étudier complètement et quantitativement ce phénomène et d'estimer les quantités d'énergie acoustique transmises et réfléchies.

L'impédance de rayonnement elle est : https://www.techniques-ingenieur.fr/bas ... es-te5132/

http://electroacoustique.univ-lemans.fr ... 14bis.html

L’impédance de rayonnement est donc la grandeur qui caractérise le mieux les quantités d’énergie mises en jeu. Son expression peut être établie facilement dans quelques cas simples qui donnent lieu à des modèles très utilisés.

Outre l’impédance de rayonnement, ces modèles sont caractérisés par des lois de répartition de l’énergie rayonnée qui leur sont propres. Ces lois sont traduites par des représentations graphiques appelés diagrammes de directivité.

Il y a donc évidemment une notion de directivité.

EDIT : correction, merci Bachi

[ohl]

Nous cherchons à savoir 2 choses, si une chambre de compression augmente le rendement ou quel agit simplement sur la sensibilité en concentrant l'énergie acoustique dans un angle plus restreint, et idem pour les pavillons.

Bonjour tous, je pense que les réponses ont été données précédemment mais un peu cachées dans les équations.
Je vais essayer d'apporter ma petite contribution à cette question intéressante.

- pour un haut-parleur, la membrane/bobine est lourde par rapport à l'air (les impédances acoustiques sont très différentes) ce qui entraine un rendement faible.
- par contre, une chambre de compression ferme en grande partie la surface d'émission ce qui augmente l'impédance vue par la membrane et se traduit par un rendement accru
- le volume d'air global mu par la membrane reste le même mais passe seulement par les petites ouvertures de la pièce de phase avec une vélocité accrue (moins de surface donc plus de vitesse)
- ensuite entre la gorge du pavillon et sa bouche, il y a adaptation progressive des impédances (petite surface avec grande vitesse vers grande surface et faible vitesse)
- de plus le pavillon évite la diffraction globale de l'onde en sortie de la pièce de phase et guide vers la bouche donc avec moins de perte en diffraction (directivité accrue due à la grande surface de sortie)

Si on essaye de mettre des ordres de grandeur pour estimer chaque part du gain en rendement :
- la compression fait gagner 20dB par rapport à de la radiation directe
- l'adaptation entre la pièce de phase et le pavillon ne fait presque rien perdre
- l'intérieur du pavillon en tant que tel n'apporte ni gain ni perte
- par contre la directivité du pavillon apporte un gain d'environ 6dB sur la réponse axiale

Je ne suis pas sûr d'être si clair...mais c'est surtout pour expliquer que le rendement accru n'est pas du seulement au pavillon !

[Bachibousouk]

Une impédance acoustique c'est le rapport entre une pression (Pa) par une vitesse (m/s). Vitesse qui est de 344m/s pour le son

La vitesse correspond à la vitesse particulaire c'est-à-dire celle de la compression-détente de la tranche d'air. S'il s'agit de la vitesse de propagation de l'onde, on parle de célérité, notée c dans les équations.
Je remarque qu'ohl évoque lui la vélocité, terme qui provient certainement de l'anglais, parce que dans mon dictionnaire, vélocité est associée à rapidité !


Bachi

[ohl]

Je remarque qu'ohl évoque lui la vélocité, terme qui provient certainement de l'anglais, parce que dans mon dictionnaire, vélocité est associée à rapidité !

Effectivement, le terme utilisé "vitesse" représente la vitesse particulaire et non pas la célérité c de la propagation. Pour agrémenter un peu le language j'ai utilisé vélocité.... un anglicisme ?

[Invite107]

Bonjour à tous,

J'ai calculé le rendement (true efficiency) d'un haut-parleur à radiation directe en prenant en compte tous les paramètres le concernant.

Avant de présenter les résultats, un dernier rappel sur la valeur de la résistance de rayonnement (le terme Ra dans mon message où je présentait le schéma complet d'un HP avec les différentes parties : électrique, mécanique et acoustique). L'expression de cette résistance Ra est la suivante :

La résistance de rayonnement est le produit de la densité de l'air par la vitesse du son divisé par la surface de la membrane et en facteur d'un terme qui est la résistance de rayonnement réduite Rr et donc la courbe ci-dessus donne la valeur. Cette valeur se calcule à partir d'une fonction de Bessel dont l'argument est ka avec k le nombre d'onde et a le rayon de la membrane. Lorsque ka est petit devant un, cela signifie que le rayon de la membrane est faible devant la longueur d'onde.

On constate donc que lorsque un HP transmet une onde sonore de longueur d'onde grande en regard de sa membrane, la valeur de Rr est faible et donc le rendement également. Lorsque la surface est grande devant la longueur d'onde le terme Rr tant vers 1 et l'impédance vers celle d'un pavillon dont la section est cette surface.

Pour faire les calculs j'ai utilisé le logiciel Maple qui est un logiciel de calcul formel largement utilisé dans le milieu scientifique pour développer des équations complexes (https://fr.maplesoft.com/products/maple/new_features/)

Calcul du rendement d'une compression :

J'ai dans un premier temps calculé le rendement exact d'une compression. On trouvera l'expression dans le fichier Maple suivant : http://www.volucres.fr/AudioHighEnd/res ... ession.pdf

Pour vérifier les calculs j'ai calculé le rendement de la compression TAD2001 en fonction de la fréquence. On peut en effet comparer ce calcul à celui de Kinoshita, le concepteur de cette chambre de compression. Voici les deux courbes pour une réponse en fréquence allant de 200 à 20000 hz.

Mon calcul donne un rendement max légèrement supérieur (moins de 0.5 dB d'écart) et prédit bien la chute à 20000 hz où le rendement est autour de 0.1 %.

Calcul du rendement d'un HP :

C'était le but de l'exercice de calculer le rendement d'un HP (true efficiency) prenant en compte la valeur exacte de la résistance de rayonnement. On trouvera les calculs dans ce fichier : http://www.volucres.fr/AudioHighEnd/res ... arleur.pdf

Escobar voulait la formule, la voici (Pas est la puissance acoustique, Pt la puissance totale le rapport donnant le rendement)



Formule totalement inexploitable sans logiciel de calcul, ce à quoi on pouvait s'attendre evidemment.

Pour calculer ce rendement avec la compression Kartesian, il faut connaître l'ensemble de ses paramètres et notamment les pertes par frottement dans la suspension. J'ai calculé les termes manquant pour que cette compression utilisée avec un pavillon donne un rendement de 40% en utilisant la formule donnée par Keele. Un tel rendement est très élevé et le véritable rendement de cette compression est probablement plus faible. Mais ça ne changera rien à la démonstration. Voici les paramètres que l'on obtient :

A partir de ces paramètres, on peut tracer la courbe de rendement de ce haut-parleur rayonnant à l'air libre (fréquence de 500 hz à 20000 hz):

On constate que le rendement plafonne à 6% alors que le rendement du même HP monté en compression sur un pavillon est de 40%.

Je précise bien que tous ces calculs portent sur la puissance totale rayonnée.

CQFD

Cordialement
Jean

[Dagda]

Beau travail Jean

[Esscobar]

Bonjour tous, je pense que les réponses ont été données précédemment mais un peu cachées dans les équations.
Je vais essayer d'apporter ma petite contribution à cette question intéressante.

Bonjour et merci de ta participation

- pour un haut-parleur, la membrane/bobine est lourde par rapport à l'air (les impédances acoustiques sont très différentes) ce qui entraine un rendement faible.

Visiblement ce qui entraîne le plus de perte c'est la conversion électrique vers mécanique, comme le dis je pense tout le monde, et Jean le montre dans son modèle équivalent . Alors évidemment la MMS a une influence sur le rendement.

- le volume d'air global mu par la membrane reste le même mais passe seulement par les petites ouvertures de la pièce de phase avec une vélocité accrue (moins de surface donc plus de vitesse)

Oui, un peu comme une rivière, analogie qui fait sens et ne semble pas contradictoire, même si pour le son il ne s'agit pas d'un déplacement en tant que tel, mais d'une vibration dont l'amplitude s'accroit avec la réduction de surface .

- ensuite entre la gorge du pavillon et sa bouche, il y a adaptation progressive des impédances (petite surface avec grande vitesse vers grande surface et faible vitesse)

Logique, et cela correspond aux règles de la physique que nous avons mise en évidence

- de plus le pavillon évite la diffraction globale de l'onde en sortie de la pièce de phase et guide vers la bouche donc avec moins de perte en diffraction (directivité accrue due à la grande surface de sortie)

Oui, encore que ce ne sont pas des pertes en tant que telles (comme le sont les pertes par chaleur), car c'est du son et donc une énergie utile mais qui est gaspiller dans l'optique d'arriver aux oreilles de l'auditeur .

- l'intérieur du pavillon en tant que tel n'apporte ni gain ni perte

Le discours est déjà différents des autres, bien que je sois aussi de cette avis. Sinon signifierai que le pavillon créé de l'énergie ...

- par contre la directivité du pavillon apporte un gain d'environ 6dB sur la réponse axiale

Voilà la sensibilité augmente pour une surface précise, en concentrant plus efficacement l'énergie acoustique dans une aire plus restreinte.

- par contre, une chambre de compression ferme en grande partie la surface d'émission ce qui augmente l'impédance vue par la membrane et se traduit par un rendement accr

- la compression fait gagner 20dB par rapport à de la radiation directe

Et c'est ici que j'ai un point de désaccord et que je cherche à corriger mes dires si effectivement je suis dans l'erreur .

Car il faut toujours rester avec le postulat d'énergie totale utile (le son) avec l'énergie totale injectée (tension + courant).

Pour tension et courant tout le monde a je pense compris. Pour le son, ce sont des particules mise en vibration. Donc pour augmenter l'énergie sonore totale (donc sur un rayonnement sphérique puisque que la source peut rayonner de manière omnidirectionnelle), il faut soit pour une même amplitude de vibration augmenter le nombre de molécules en vibration, soit pour un même nombre de particules en vibration augmenter l'amplitude de vibration ... Soit les 2 combinés. Mais cela en prenant en compte toutes les directions (omni).

C'est pour cela que pour moi la chambre de compression ne peut pas augmenter le rendement, car comme tout le monde semble s'en accorder, l'équation suivante était acceptée :

Sd x Ad = Sg x Ag (S pour les surfaces et A pour l'amplitude)

Comme il y a un rapport d'égalité sans facteur qui pourrait accroitre l'énergie sonore (nombre de molécules ou amplitude de vibration). Si Ag augmente (amplitude de vibration des particules) cela signifie que Sg (Surface de gorge) diminue, ce qui implique moins de molécule en vibration...